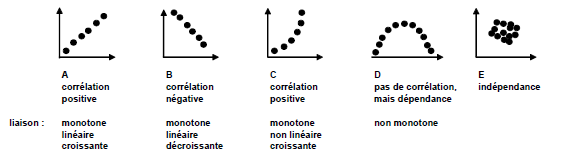
Le modèle de la régression linéaire (y = ax+b) ne convient pas toujours pour exprimer un lien entre deux variables X et Y, surtout lorsque celles-ci ne sont pas quantitatives.
Dans le cadre de variables ordinales, le test de Spearman est une alternative (basée sur les rangs) à la régression linéaire.
Le R de Spearman (coefficient de correlation de Spearman) offre un indicateur statistique de la modélisation du modèle et notamment de sa capacité à coller aux données réelles utilisées pour le construire. Le R varie entre [-1,1] et plus il s’approche de ses bornes, meilleur est le modèle.
Le test de corrélation de Spearman souffre cependant d'une limitation identique à la régression linéaire, à savoir que, s'il y a une relaion entre X et Y, celle-ci doit être monotone (soit toujours croissante ou toujours décroissante mais pas un mélange des deux).

Le test de correlation de Spearman permet, en outre, de vérifier la validité d'un modèle pour lequel R serait ≠ 0.
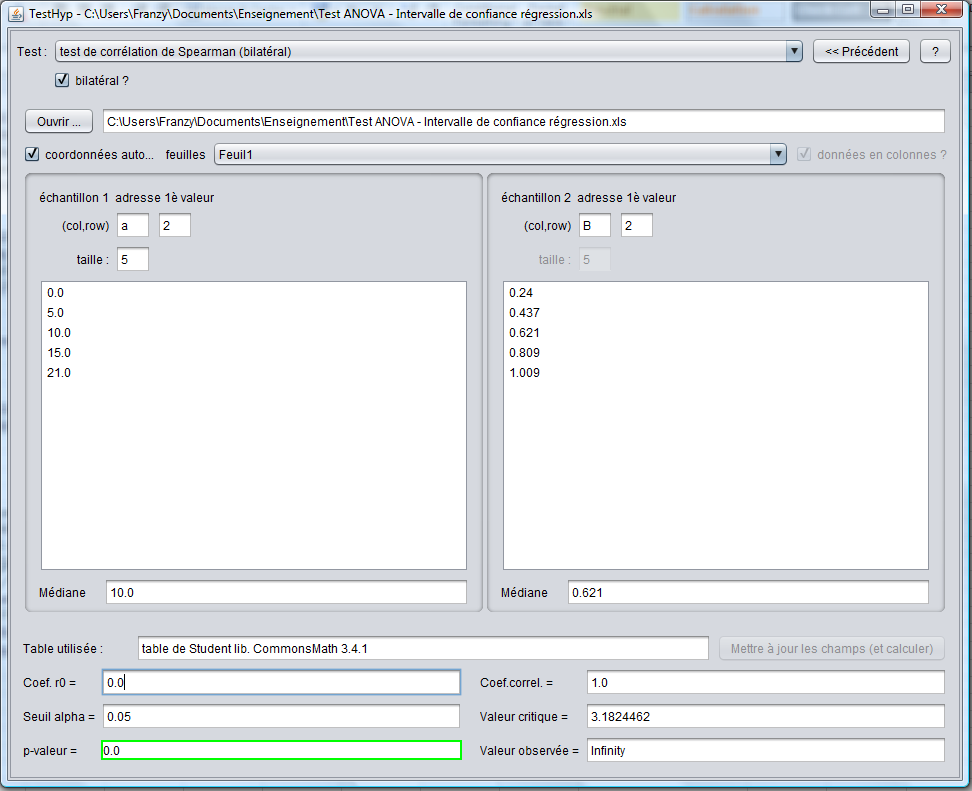
Comme on peut le voir sur l'exemple ci-dessus, le test de Spearman étant basé sur les rangs, présente la faiblesse de donner un résultat r = 1 (et donc une pval = 0) si chaque couple (Xi,Yi) se classe sans ambigüité l'un par rapport à l'autre.