La régression linéaire permet de modéliser une variable réponse Y continue à partir d’une matrice de P variables explicatives X1, X2, ... XP continues.
Le modèle associé à la régression linéaire s’exprime au travers de la formule suivante,
Y = β0 + β1 X 1 + ... + βP X P + ε
La plus populaire de toutes les méthodes d'estimation des coefficients β demeure celle des moindres carrés.
Le R2 (ou coefficient de détermination) offre un indicateur statistique de la modélisation du modèle et notamment de sa capacité à coller aux données réelles utilisées pour le construire. Le R2 varie entre [0,1] et plus il s’approche de sa borne supérieure, meilleur est le modèle.
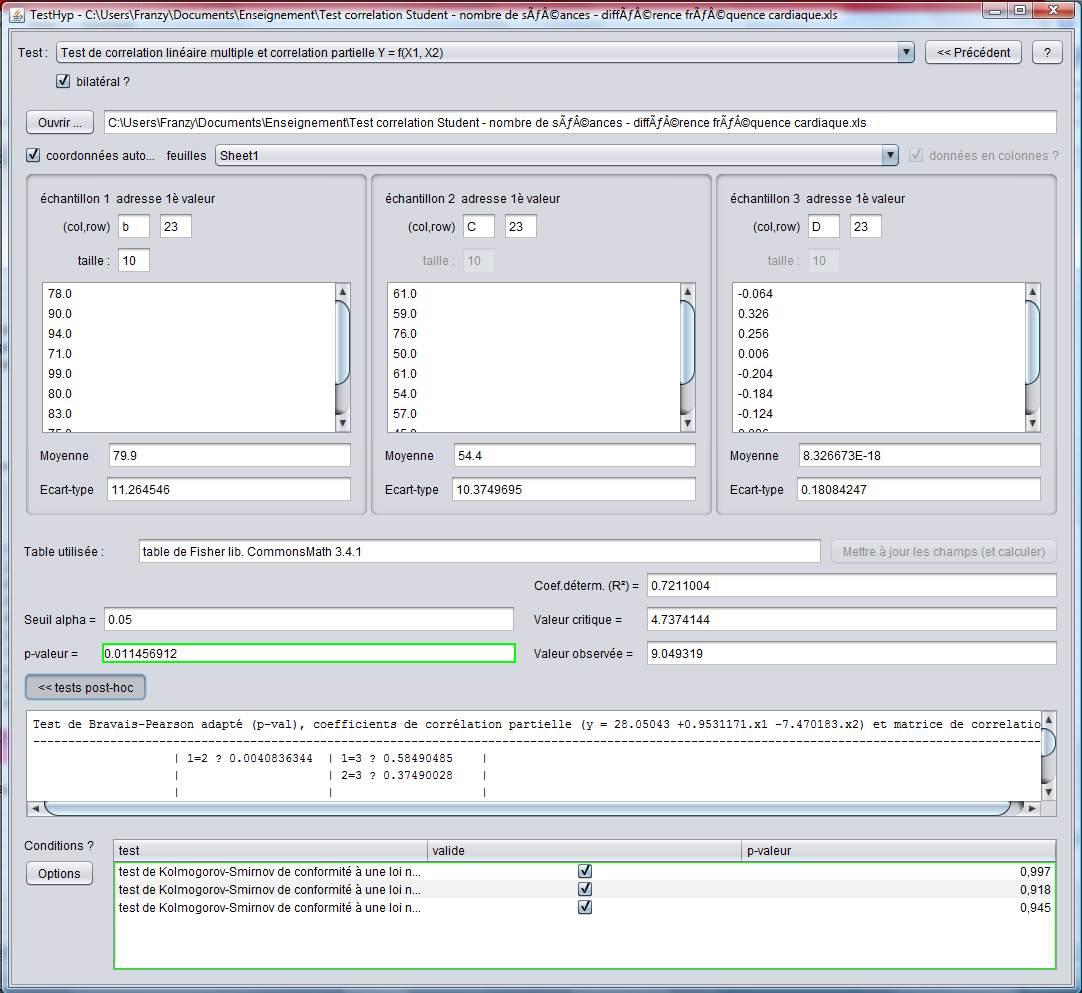
Le test de corrélation multiple et de régression multiple permettent tous deux de tester la validité du modèle dans sa globalité. Le test de régression permet, en outre, de vérifier l'incidence de telle ou telle variable sur le modèle (le modèle est-il meilleur si l'on ne prend pas en compte la variable Xi ?) tandis que le test de corrélation permet de comparer les différentes relations de dépendance entre les variables, prises 2 à 2 (Y vs X1, Y vs X2, X1 vs X2, ...), les autres étant considérées comme constantes.

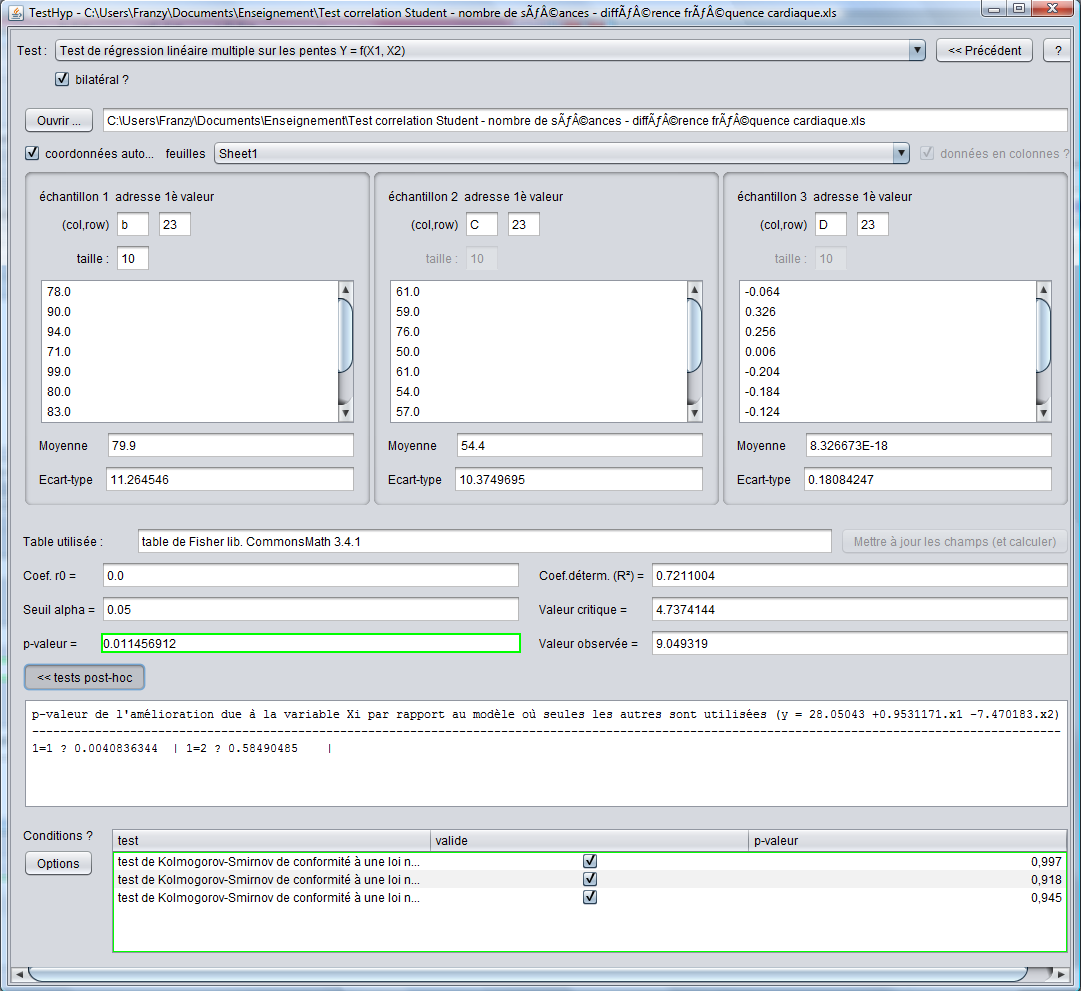
Comme nous pouvons le voir sur les images ci-dessus, les résultats des tests pos-hoc de corrélation et de régression présentent des résultats similaires vis-à-vis de Y vs X1 et Y vs X2, ce qui est logique étant donné que le test de corrélation compare 2 des variables considérant la 3è comme inexistante tandis que le test de régression compare le modèle "sans l'une des variables" avec le modèle comprenant toutes les variables. Dans un cas de figure à 3 variables X, les résultats seraient différents : le cas de la corrélation reviendrait à comparer le modèle où 2 des variables ont été exclues tandis que le test de régression comparerait le modèle où seulement l'une des variables a été exclue.
Par ailleurs, avec un modèle du type Y = f(X) comprenant une seule variable X, ces tests donnent des résultats identiques au test de Bravais-Pearson.
Si la condition de normalité n'est pas respectée, on s'orientera vers un test non-paramétrique (pour variable indépendante ordinale) tel que le test de Spearman ou la régression logistique.