On cherche à comparer les médianes &xi1, &xi2, ..., &xik de k échantillons indépendants. On veut savoir si le fait qu'au moins l'une des médianes &xii différe des autres est dû au hasard ou à, par exemple, la technique employée.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être qualitative ordinale.
Les effectifs des k échantillons ne sont pas forcément identiques.
Exemple :
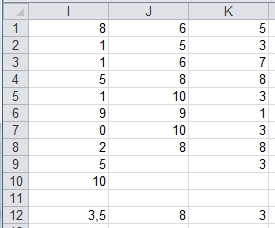
Pour étudier l'influence d'un traitement, on prélève au hasard 27 personnes désireuses de participer à cette étude et on les répartit aléatoirement dans 3 groupes distincts. On applique le traitement A au groupe 1, le traitement B au groupe 2 et le traitement C au groupe 3. A l'issue des traitements, on demande à chaque participant d'estimer son bien-être sur une échelle de 1 à 10 :

Constate-t-on une différence significative entre les 3 traitements (au seuil 95%) ?
Le programme nous fournit les données suivantes :
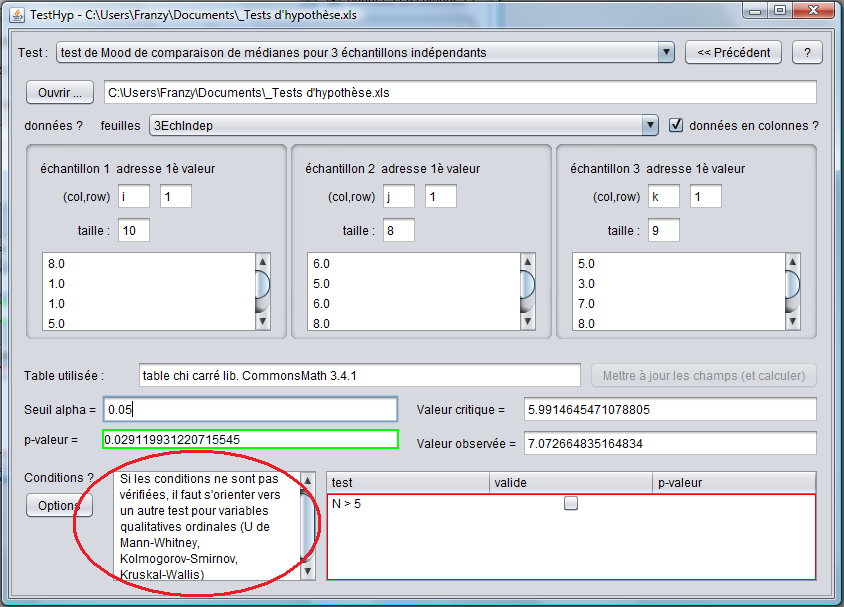
Nous pouvons voir que, bien que la pval soit < au seuil α, nous ne pouvons pas nous fier aux résultats du test car la condition portant sur la taille de l'échantillon n'est pas vérifiée.
Cette condition peut paraître contradictoire vu que la taille des 3 échantillons est respectivement de 10, 8 et 9. Cependant, pour réaliser les calculs qui y sont associés, le test de Mood construit une table de contingence reprenant le nombre de valeurs se répartissant de part et d'autre de la médiane pour ensuite appliquer un test χ² qui doit vérifier cette condition.
