On s'intéresse à k variables X_1, X_2, ... X_k dans k populations distinctes. On désire mettre en évidence le fait qu'au moins une de ces k variables a tendance à prendre de plus grandes ou de plus petites valeurs que les autres variables.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être qualitative ordinale.
Les effectifs des k échantillons ne sont pas forcément identiques.
Exemple :
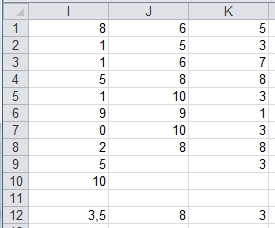
Pour étudier l'influence d'un traitement, on prélève au hasard 27 personnes désireuses de participer à cette étude et on les répartit aléatoirement dans 3 groupes distincts. On applique le traitement A au groupe 1, le traitement B au groupe 2 et le traitement C au groupe 3. A l'issue des traitements, on demande à chaque participant d'estimer son bien-être sur une échelle de 1 à 10 :

Constate-t-on une différence significative entre les 3 traitements (au seuil 95%) ?
Le programme nous fournit les données suivantes :
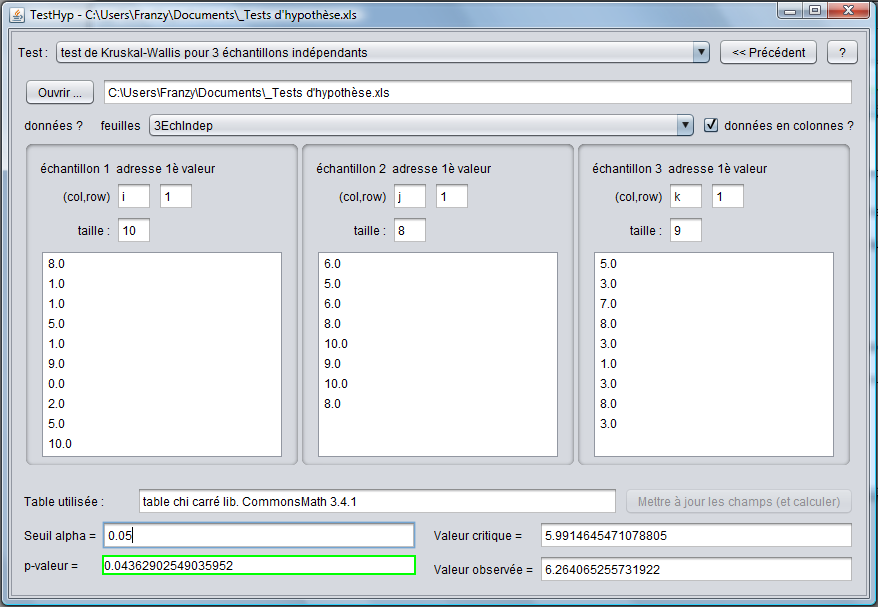
Nous pouvons voir que la pval est < au seuil α. Donc, au seuil 95%, il existe une différence significative entre les traitements.