On désire tester l'hypothèse selon laquelle une variable possède la même distribution dans k populations différentes et si la différence observée est imputable aux fluctuatons d'échantillonnage (ce test peut donc s'utiliser également comme un test d'adéquation ou d'association).
Où πij = proportion d'éléments dans la population i chez qui la variable prend une valeur appartenant à la modalité ou catégorie Cj de la variable dépendante.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être (rendue) catégorielle : c'est-à-dire qualitative nominale ou ordinale, quantitative mesurée sur des échelles d'intervalles ou de rapports subdivisées en différentes classes.
Les effectifs des k échantillons ne sont pas forcément identiques.
Exemple :
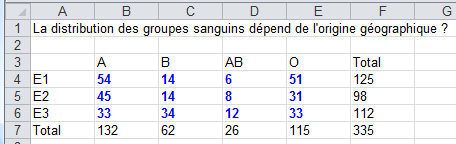
Les groupes sanguins A, B, O et AB ont été déterminés dans 3 échantillons (E1 : France ; E2 : Roumanie ; E3 : Proche-Orient) d'hommes adultes.

Cette observation est-elle conforme à l'hypothèse selon laquelle la répartition des groupes sanguins dépend d'un facteur géographique au seuil 95% ?
Le programme nous fournit les données suivantes :
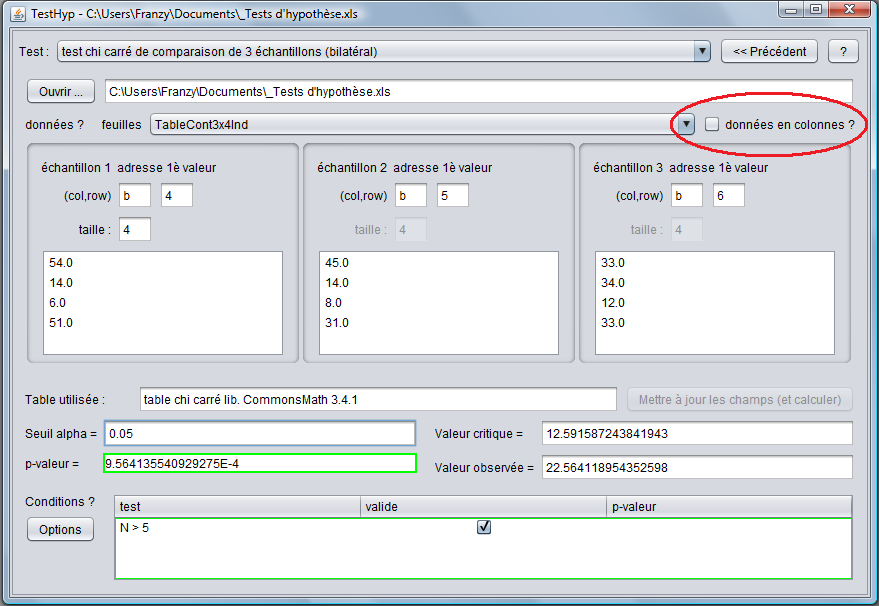
Nous pouvons voir que la pval est < au seuil α donc l'hypothèse de l'égalité des proportions peut être rejetée.