On cherche à comparer les écart-types σ1 et σ2 de deux populations. On veut savoir si le fait que σ1 soit différent de σ2 est dû au hasard ou à, par exemple, la technique employée.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être quantitative.
Les effectifs des deux échantillons ne sont pas forcément identiques.
La condition de normalité des échantillons doit être vérifiée.
Exemple :
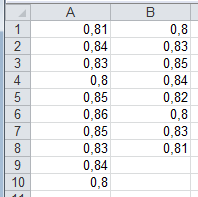
Pour étudier un lot de fabrication de comprimés, on prélève au hasard 10 comprimés produits par la chaîne n°1 et 8 comprimés produits par la chaîne n°2. On les pèse. On observe les valeurs de poids en grammes :

Les chaînes n°1 et n°2 produisent-elles les mêmes comprimés ? La différence observée est-elle significative au seuil 95% ?
Le programme nous fournit les données suivantes :
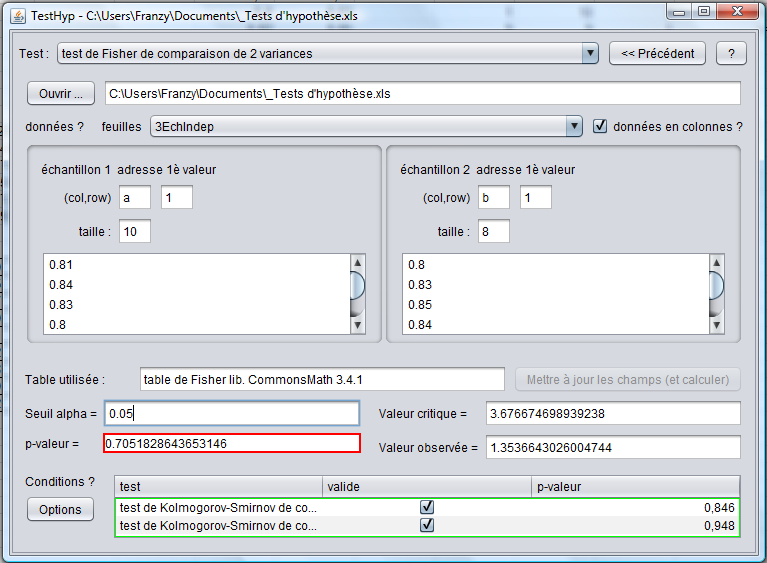
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des variances ne peut être rejetée. L'écart-type du poids de l'échantillon de la chaîne n°1 est identique à celui de la chaîne n°2.
Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.
En outre, les conditions de normalité sont vérifées, ce qui permet de conclure quant au test de Fisher mais qui induit également une erreur β.