On désire tester l'hypothèse selon laquelle une variable possède la même distribution dans k populations différentes et si la différence observée est imputable aux fluctuatons d'échantillonnage (ce test peut donc s'utiliser également comme un test d'adéquation ou d'association).
Où πij = proportion d'éléments dans la population i chez qui la variable prend une valeur appartenant à la modalité ou catégorie Cj de la variable dépendante.
Ce test est bilatéral.
Comme pour le test χ², la variable dépendante doit être (rendue) catégorielle : c'est-à-dire qualitative nominale ou ordinale, quantitative mesurée sur des échelles d'intervalles ou de rapports subdivisées en différentes classes.
Les effectifs des k échantillons ne sont pas forcément identiques.
A la différence du test χ², le test de Fisher est adapté pour les petits échantillons. En outre, les calculs associés dépassent vite les capacités de calcul d'un ordinateur conventionnel lorsque les effectifs des échantillons sont trop importants.
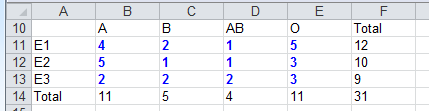
Exemple :
Les groupes sanguins A, B, O et AB ont été déterminés dans 3 échantillons (E1 : France ; E2 : Roumanie ; E3 : Proche-Orient) d'hommes adultes.

Cette observation est-elle conforme à l'hypothèse selon laquelle la répartition des groupes sanguins dépend d'un facteur géographique au seuil 95% ?
Le programme nous fournit les données suivantes :
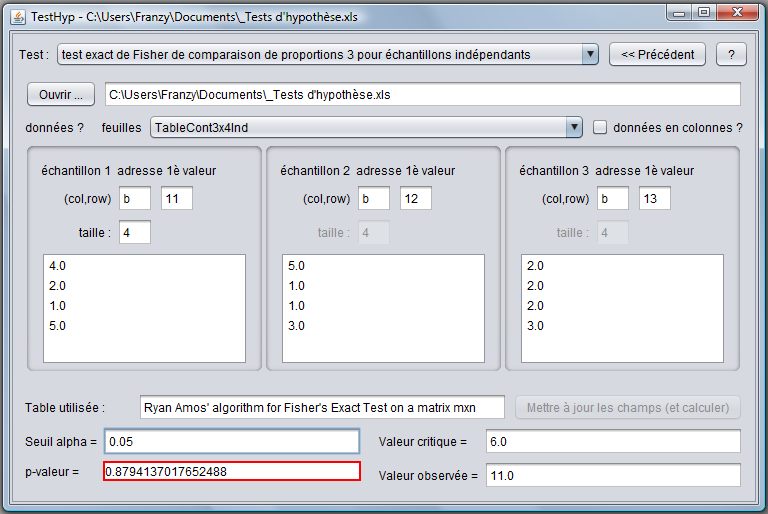
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des proportions ne peut pas être rejetée. Ce faisant, nous introduisons également une erreur β.