Test χ² de conformité d'une distribution

On désire tester l'hypothèse selon laquelle une variable possède une distribution théorique donnée et si la différence observée est imputable aux fluctuatons d'échantillonnage (ce test peut donc s'utiliser également comme un test d'adéquation ou d'association).

• H₀ : ∀ j ∈ {1, 2, ... J} : π_j = π_j0 (les proportions sont identiques)
• H₁ : ∃ j ∈ {1, 2, ... J} : π_j ≠ π_j0 (il existe au moins une proportion qui diffère)

Où π_j = proportion d'éléments dans la population chez qui la variable prend une valeur appartenant à la modalité ou catégorie C_j de la variable dépendante.


Ce test peut être bilatéral ou unilatéral.

La variable dépendante doit être (rendue) catégorielle : c'est-à-dire qualitative nominale ou ordinale, quantitative mesurée sur des échelles d'intervalles ou de rapports subdivisées en différentes classes.

L'échantillon doit être unique car il s'agit d'un test de conformité.


Exemple 1 :

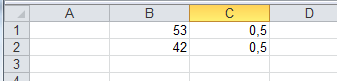
Sur 95 naissances, on relève 53 garçons.

Cette observation est-elle conforme à l'hypothèse selon laquelle la probabilité d'avoir un garçon à la naissance est de 0,5 au seuil 95% ?


Le programme nous fournit les données suivantes :

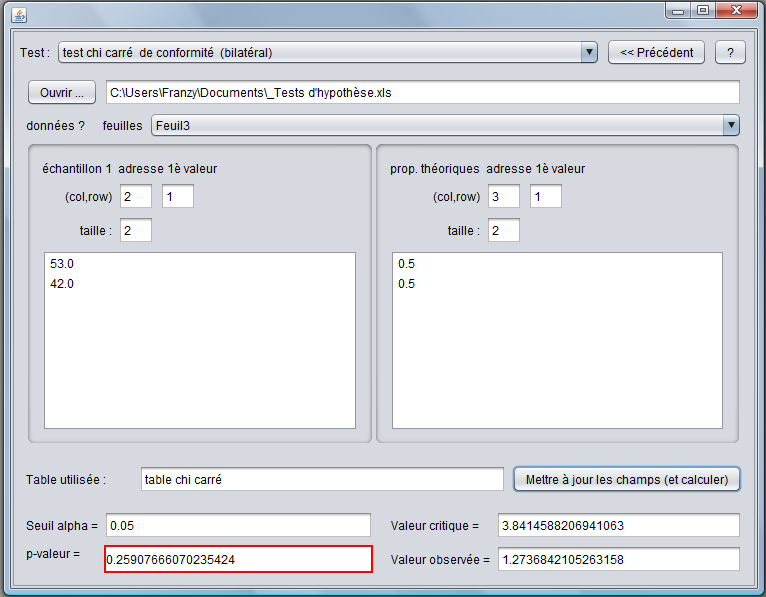
Nous pouvons voir que la p_val est > au seuil α donc l'hypothèse de l'égalité des proportions ne peut être rejetée. L'observation ne permet donc pas de rejeter l'hypothèse selon laquelle la probabilité d'avoir un garçon à la naissance est de 0,5.

Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.

Exemple 2 :

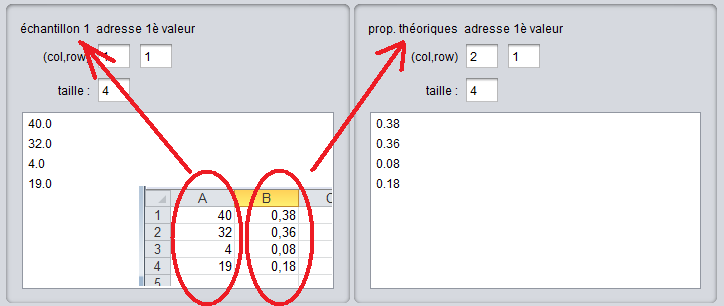
Sur 95 prises de sang, on relève 40 A+, 32 O+, 4 B+ et 19 autres (AB+, O-, A-, B-, AB-).

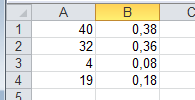
Cette observation est-elle conforme à l'hypothèse selon laquelle la répartition des groupes sanguins est de 38% de A+, 36% de O+, 8% de B+ et 18% d'autres, au seuil 95% ?


Le programme nous fournit les données suivantes :

Nous pouvons voir que la p_val est > au seuil α donc l'hypothèse de l'égalité des proportions ne peut être rejetée. L'observation ne permet donc pas de rejeter l'hypothèse selon laquelle au moins l'une des proportions se distingue des autres.

Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.

Remarque

Veillez à ce que la somme des proportions théoriques soit bien égale à 1, ainsi qu'à renseigner ces dernières sous forme de nombre décimaux ou de pourcentages sur le feuillet Excel :

< Précédent   Retour à la table des matières   Suivant >