On s'intéresse à l'effet d'un facteur de variabilité A sur une variable X dont les différentes mesures sont considérées comme le facteur B. On désire mettre en évidence le fait que la variable X a tendance à prendre de plus grandes ou de plus petites valeurs sous l'effet de ce facteur A.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être quantitative.
Les effectifs des k échantillons sont identiques.
Exemple :
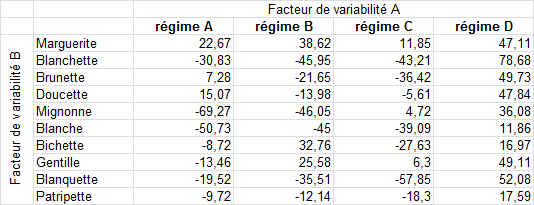
Pour déterminer si un certain type d'alimentation a de l'impact sur la production de lait, on s'intéresse à la différence par rapport à la moyenne de l'élevage de la production de lait mensuelle en L d'un groupe de vaches nourries alernativement selon 4 mélanges A, B, C puis D différents. Les données sont regroupées dans le tableau suivant :

On constate que les moyennes sont différentes. Les différences observées sont-elles imputables au type d'aliment au seuil 95% ?
Le programme nous fournit les données suivantes :

Nous pouvons voir que la pvalA est < au seuil α donc le type d'aliment a une influence significative sur la production de lait. Nous pouvons également voir que la pvalB est significative, ce qui signifie que le facteur B a également de l'influence. Mais dans le cadre de cette étude, conclure que la producion de lait est influencée par la vache (indépendamment du régime) me paraît un peu trivial.
Pour déterminer quels sont précisément les aliments qui se démarquent, il faut comparer les échantillons 2 à 2 à l'aide, par exemple, de tests de Student.
En outre, la condition d'égalité des variances n'est pas vérifiée, ce qui ne permet pas de conclure quant au test ANOVA.
Si la condition de normalité n'est pas respectée, on s'orientera vers un test non-paramétrique (pour variable indépendante ordinale) tel que le test de Friedman de comparaison de médianes pour k échantillons appariés.
Il faudra cependant veiller à nuancer l'interprétation des résultats en prenant en compte qu'un test basé sur les rangs compare la médiane plutôt que l'influence d'un facteur.