On cherche à comparer les moyennes &mu1 et &mu2 de deux populations distinctes. On veut savoir si le fait que &mu1 soit différent de &mu2 est dû au hasard ou à, par exemple, la technique employée.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être quantitative.
Les effectifs des deux échantillons ne sont pas forcément identiques.
Exemple :
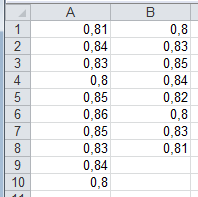
Pour étudier l'influence d'un traitement, on prélève au hasard 18 personnes désireuses de participer à cette étude et on les répartit aléatoirement dans 2 groupes distincts. On applique le traitement A au groupe 1 et le traitement B au groupe 2. On observe des valeurs de variation de poids en kg :

La différence de poids observée entre les 2 groupes est-elle significative au seuil 95% ?
Le programme nous fournit les données suivantes :
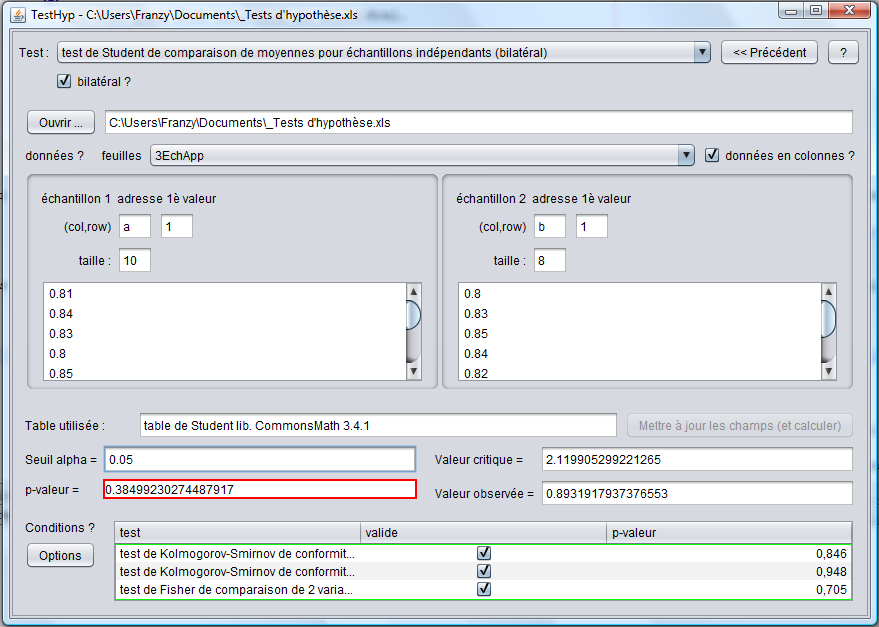
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des moyenne ne peut être rejetée. La variation de poids moyen entre nos 2 groupes d'étude n'est donc pas significative.
En outre, les conditions de normalité et d'égalité des variances sont vérifées, ce qui permet de conclure quant au test de Student mais qui induit également une erreur β.
Si la condition de normalité n'est pas respectée, on s'orientera vers un test non-paramétrique (pour variable indépendante ordinale) tel que le test du U de Mann-Whitney de comparaison de médianes pour 2 échantillons indépendants.
Il faudra cependant veiller à nuancer l'interprétation des résultats en prenant en compte qu'un test basé sur les rangs compare la médiane plutôt que la moyenne.
Si seule la condition d'égalité des variances n'est pas respectée, on s'orientera vers un test t de Welsh de comparaison de moyennes pour 2 échantillons indépendants.