Ce test est la généralisation du test de MacNemar. Le test est significatif si la distribution (ou la proportion) issue d'un des échantillons présente une différence significative par rapport à la distribution (ou proportion) de l'autre échantillon.
Soit la table de contigence suivante, établie sur base de l'échantillon de k-uples (X1,... Xk)
| Situation 1 | |||||
|---|---|---|---|---|---|
| Critère 1 observé | Critère 2 observé | ... | Critère k observé | ||
| Situation 2 | Critère 1 observé | n00 | n01 | ... | n0k |
| Critère 2 observé | n10 | n11 | ... | n1k | |
| ... | ... | ... | ... | ... | |
| Critère k observé | nk0 | nk1 | ... | nkk | |
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être nominale (binaire ou non).
Les effectifs des deux échantillons sont identiques étant donné que nous disposerons les résultats dans un tableau de k fois k valeurs.
Exemple 1 :
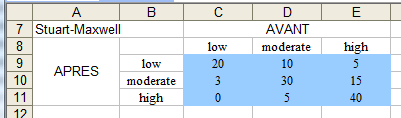
128 sujets ont été questionnés sur leurs douleurs au dos, à deux moments, avant un certain traitement et après ce même traitement. On a noté la réponse du sujet aux deux moments avant et après. Ainsi, nous avons obtenu le tableau suivant (ex : 10 sujets ressentaient une douleur modérée avant et légère après)

Constate-t-on une différence entre la situation "avant" et "après" au seuil 95% ?
Le programme nous fournit les données suivantes :
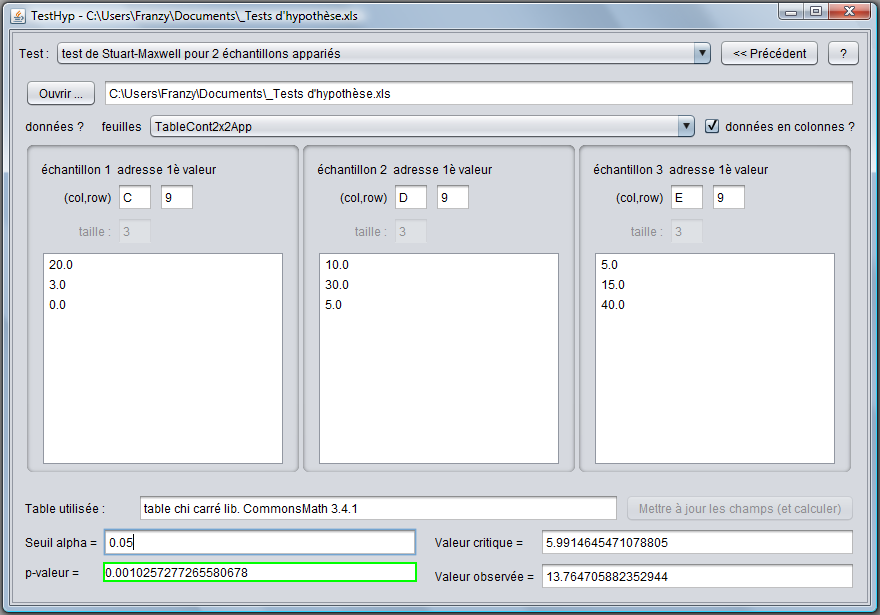
Nous pouvons voir que la pval est < au seuil α et donc nous pouvons rejeter l'hypothèse initiale au seuil 95%. Il existe donc une différence significative entre les distributions des proportions avant et après.
Exemple 2 :
On compare le nombre d'échecs à un test de résistance physique passé avant une période d'entraînement, au milieu de cette période et en fin de période. Les résultats effectués sur les participants ont été résumés dans le tableau ci-dessous :
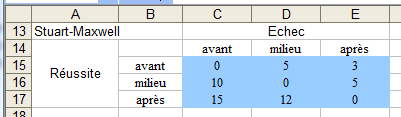
Constate-t-on une différence entre la proportion d'échec et de réussite au seuil 95% ?
Le programme nous fournit les données suivantes :
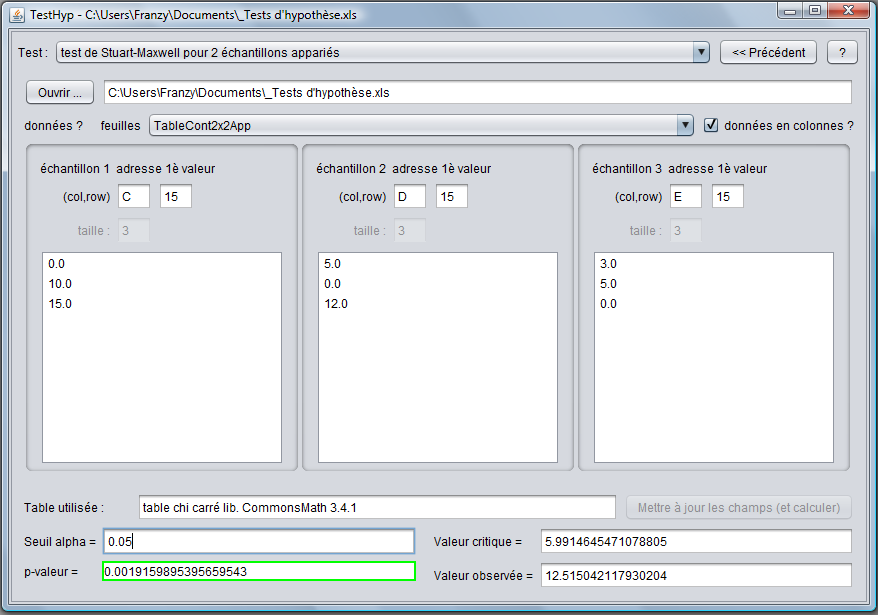
Nous pouvons voir que la pval est < au seuil α et donc nous pouvons rejeter l'hypothèse initiale au seuil 95%. Il existe donc une différence significative entre les distributions des proportions d'échec et de réussite.