La régression linéaire permet de modéliser une variable réponse Y continue à partir d’une variable explicative X continue.
Le modèle associé à la régression linéaire s’exprime au travers de la formule suivante,
Y = aX + B + ε
La plus populaire de toutes les méthodes d'estimation des coefficients a et b; demeure celle des moindres carrés.
Le R (ou coefficient de correlation) offre un indicateur statistique de la modélisation du modèle et notamment de sa capacité à coller aux données réelles utilisées pour le construire. Le R varie entre [-1,1] et plus il s’approche de ses bornes, meilleur est le modèle.
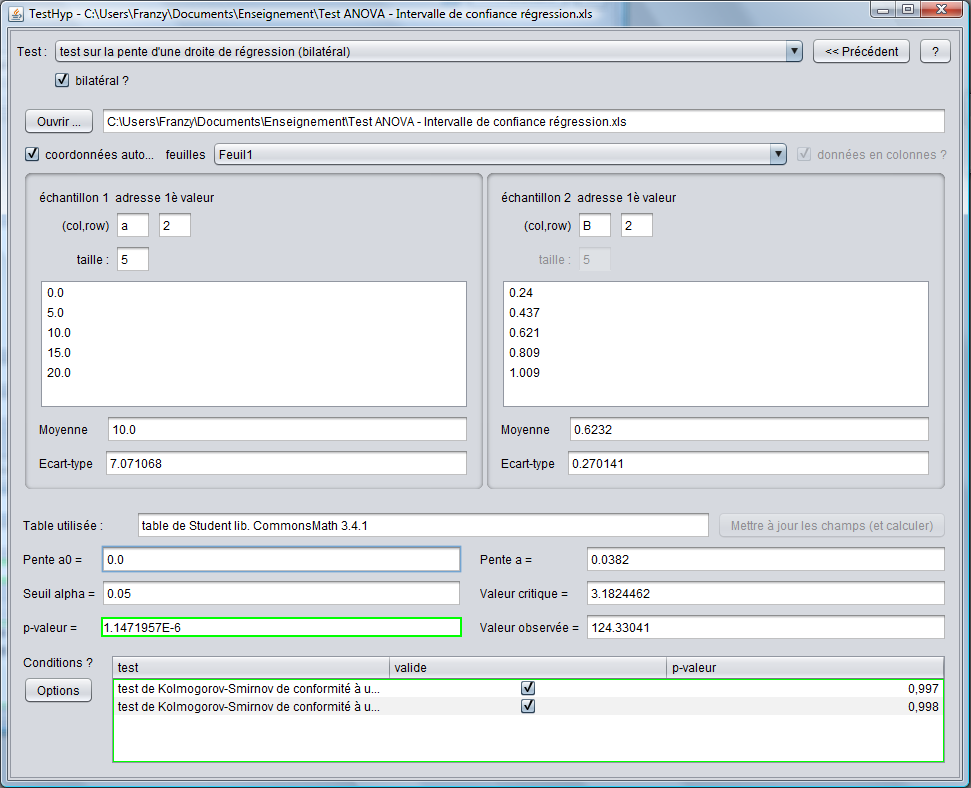
Le test de régression sur la pente permet de tester la validité du modèle par rapport au modèle Y "constant" où a est = à 0 (H0). Le test de régression permet, en outre, de vérifier la validité d'un modèle pour lequel a serait ≠ 0.

Par ailleurs, avec un modèle du type H0 : a = 0, ce test donne des résultats identiques au test de Bravais-Pearson sur le coefficient de correlation pour lequel H0 : R = 0. Le test relatif à l'ordonnée à l'origine donnera une valeur différente étant donné que ce test compare la validité du modèle sans ordonnée à l'origine (Y = aX) avec l'original, tandis que le test de la pente compare la validité du modèle sans prendre la variable X en compte (Y = b) avec l'original.
Si la condition de normalité n'est pas respectée, on s'orientera vers un test non-paramétrique (pour variable indépendante ordinale) tel que le test de Spearman ou la régression logistique.