On cherche à comparer les distributions de l'échantillon à une loi normale. Ce test compare les fréquences cumulées F(x) des valeurs x l'échantillon avec la fonction de répartition de la loi normale F0(x). Autrement dit, ce qui revient à comparer plus spécifiquement la position des moyennes ou médianes ainsi que la dispersion des résultats.
Ce test est bilatéral.
La variable dépendante doit être qualitative ordinale.
L'échantillon doit être unique car il s'agit d'un test de conformité.
Exemple :
Pour étudier un lot de fabrication de comprimés, on prélève au hasard 10 comprimés parmis la population des 30 000 comprimés produits et on les pèse. On observe les valeurs de poids en grammes :

On sait que le poids moyen de la production est de 0,83g. Le poids moyen observé dans l'échantillon prélevé est-il compatible avec la valeur moyenne de la production au seuil 95% ?
Le programme nous fournit les données suivantes :
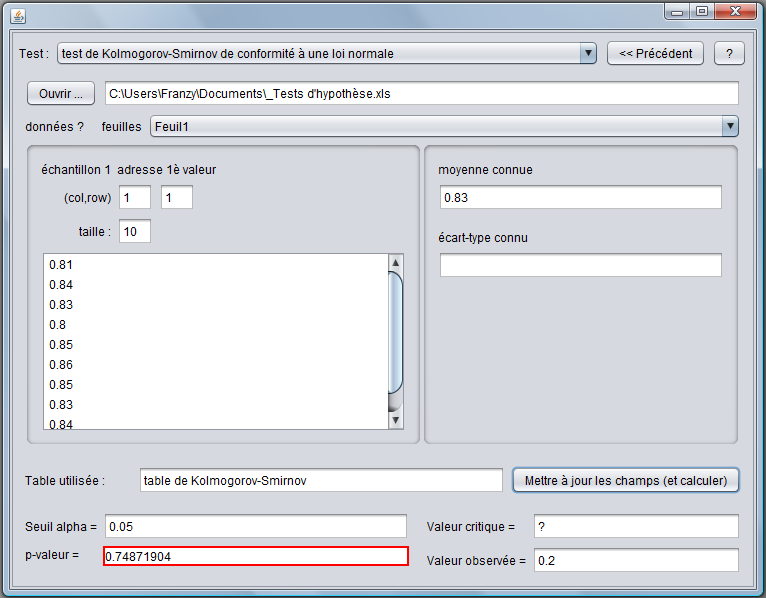
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des moyennes ne peut être rejetée. Le test de Kolmogorov-Smirnov va un peu plus loin en affirmant que la distribution des poids de l'échantillon des 10 comprimés est conforme à une distribution normale de moyenne 0,83 g.
Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.
Reprenons les données précédentes et supposons un écart-type σ0 connu.
On sait que le poids moyen de la production est de 0,83g et que l'écart-type σ0 = 0,01. Le poids moyen observé dans l'échantillon prélevé est-il compatible avec la valeur moyenne de la production au seuil 95% ?
Le programme nous fournit les données suivantes :
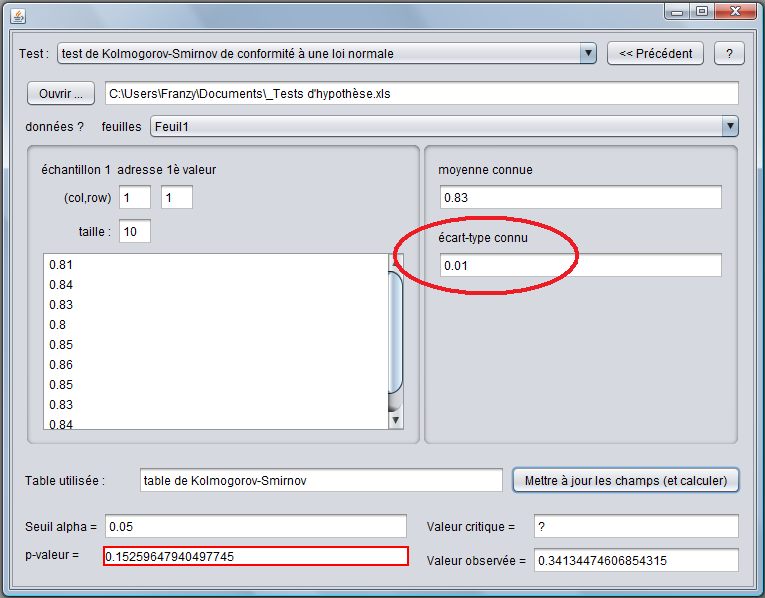
Nous pouvons voir que les conclusions restent identiques.