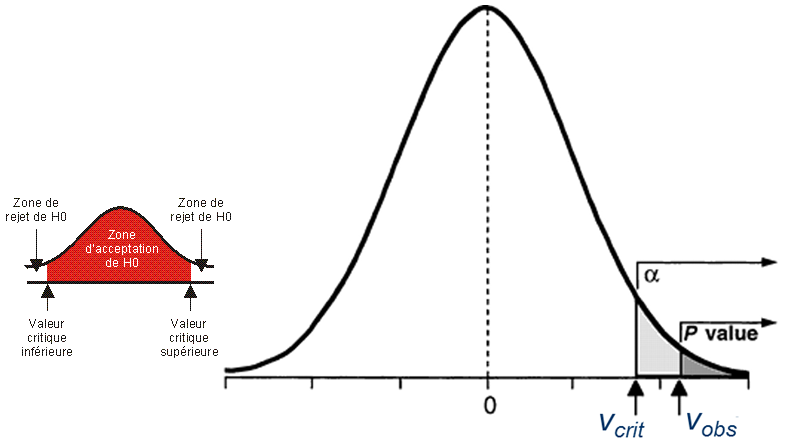
Généralement, les logiciels de statistique donnent la p-valeur. On rejette alors l'hypothèse nulle au niveau de signification choisi (par exemple α = 0,05) si (et seulement si) la p-valeur est inférieure ou égale au niveau de signification choisi (pval = 0,003 < α = 0,05, rejet d'H0).
En d'autres termes, dans le cadre d'un test unilatéral, on rejette donc l'hypothèse initiale (H0) si vobs > vcrit ou, de façon équivalente, si pval < α (voir plus loin). Le calcul de vobs et la détermination de la borne vcrit est dépendante du test considéré.
Dans le cas d'un test bilatéral, on rejette H0 si vobs < vcrit,inf ou vobs > vcrit,sup ou, de façon équivalente, si pval < α/2 [à vérifier dans le cas de distribution non symétriques (χ² ...)].

Par ailleurs, les tests statistiques et le degré de signification p (= pval) font souvent l'objet d'interprétations erronées.
Ainsi, on dit fréquemment à l'issue d'un test de comparaison des moyennes statistiquement significatif qu'il y a 95% (= 1-α) de chances pour que les moyennes soient différentes. Il convient de nuancer car les moyennes des populations sont des constantes et non des variables aléatoires (au contraire de la moyenne d'un échantillon choisi au hasard au sein de cette population).
Remarquons à ce titre que la pval peut elle-même être vue comme une variable aléatoire. La pval, qui dépend donc des échantillons, n'est pas relative à la différence entre les moyennes des populations mais bien au jugement que l'on émet au sujet de l'égalité de ces moyennes. Tout ce que l'on peut dire, en concluant à l'existence d'une différence avec un test statistiquement significatif, c'est que l'on a 5% de chances seulement d'aboutir à une telle conclusion par le simple fait du hasard (et donc de se tromper en rejetant H0).
En toute rigueur, il n'est pas possible non plus de dire que la pval représente la probabilité que les résultats de l'essai soient dus à la chance. En fait, la pval est la probabilité d'observer un résultat sous l'hypothèse que seule la (mal)chance ou les fluctuations d'échantillonnage expliquent ce résultat.
Ce n'est pas non plus la probabilité de l'absence de différence. La pval est la probabilité d'observer un résultat en l'absence de différence, ce n'est pas la probabilité qu'il n'y ait pas de différence compte tenu du résultat observé.
Quoi qu'il en soit, si H0 est acceptée, le risque de première espèce (α) est sans objet. On peut toujours essayer de calculer le risque de deuxième espèce. Mais ce problème possède rarement une solution simple et l'on perd souvent de vue l'existence même de ce risque.
La plupart du temps, en cas de rejet de H0, on se contente de préciser l'importance du risque de première espèce, sans se soucier de l'existence d'une seconde possibilité d'erreur introduite lors de la vérification des conditions.