Un échantillon est un sous-ensemble de la population étudiée.
La distribution d'échantillonnage est une distribution théorique. Par exemple, celle que l'on obtiendrait si nous prenions tous les échantillons possibles de même taille tirés chacun au hasard de la même population. Autrement dit, c'est la distribution sous H0, de toutes les valeurs possibles qu'une statistique (ou variable statistique, la moyenne par exemple) peut avoir lorsque cette statistique est calculée à partir d'échantillons de même taille tirés au hasard.
L'échantillonnage a pour but de fournir suffisamment d'informations pour pouvoir faire des déductions sur les caractéristiques de la population. Mais bien entendu, les résultats obtenus d'un échantillon à l'autre vont être en général différents et différents également de la valeur de la caractéristique correspondante dans la population. On dit qu'il y a des fluctuations d'échantillonnage. Comment, dans ce cas, peut-on tirer des conclusions valables ? En déterminant les lois de probabilités qui régissent ces fluctuations.
Par exemple, dans le jeu de « pile ou face », quelle est la probabilité d'obtenir trois « face » lorsque trois pièces de monnaie sont lancées simultanément.
Le nombre total d'événements possibles est de huit (combinaisons possibles de face et de pile) :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| Pièce 1 | F | F | F | F | P | P | P | P |
| Pièce 2 | F | F | P | P | F | F | P | P |
| Pièce 3 | F | P | F | P | F | P | F | P |
Sur les huit possibilités, une seule correspond à l'événement attendu : l'apparition simultanée de trois faces. Ainsi la probabilité sous H0 d'avoir trois faces simultanément lors d'un lancé de trois pièces est de 1⁄8. Cela est mis en évidence par la distribution d'échantillonnage de tous les événements possibles. Cependant, cette méthode n'est réalisable que pour de petits échantillons. Pour des échantillons plus importants, il faut faire appel à des modèles mathématiques. Ces derniers impliquent des contraintes, généralement portant sur la distribution de la population et/ou sur la taille de l'échantillon. Aussi lorsque l'on utilise ces théorèmes nous devons tenir compte de leurs contraintes inhérentes.
Considérons l'exemple de la comparaison de deux méthodes A et B utilisées pour améliorer l'orthographe. Les échantillons 1 et 2 sont constitués d'élèves. La méthode A est appliquée au groupe 1 et la méthode B au groupe 2.
Ensuite, consécutivement à un test d'orthographe, nous constatons que les résultats du groupe 1 sont meilleurs. La méthode A est-elle plus efficace que la B ?
Nous constatons un problème évident : les résultats sont différents si l'on recommence l'expérience avec d'autres élèves.
Dès lors, nous pouvons considérer la différence des moyennes des deux échantillons (par facilité, appelons « vobs » cette différence) comme une variable aléatoire (par définition, puisqu'on ne connaît pas sa valeur avant d'avoir réalisé l'expérience). Par conséquent, une modélisation mathématique de vobs est possible.
Remarquons que certains tests statistiques nécessitent une condition particulière sur la distribution d'échantillonnage (par exemple, la distribution doit être normale ; nous y reviendrons plus loin).
Cela dit, pour comprendre ce qui suit, supposons que cette variable aléatoire vobs ait par exemple une distribution normale.
Considérons deux cas de figure : soit vobs est proche du centre de cette distribution, soit vobs en est éloignée.
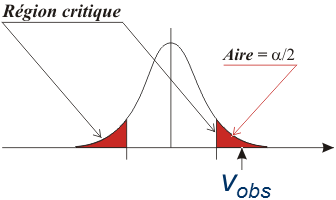
Arbitrairement, définissons une région critique telle que si vobs s'y trouve, nous considérons (toujours arbitrairement) que la différence observée entre les deux moyennes est trop importante pour être due au hasard.
Evidemment, il persiste une possibilité que le résultat obtenu soit en réalité dû au hasard mais, plus la région critique est étroite, plus c'est improbable (ça ne serait vraiment pas de chance).

La valeur vobs se calcule différemment pour chaque test d'hypothèse. Pour un test de comparaison de deux moyennes, elle est proportionnelle à la différence entre les moyennes des deux échantillons comparés. Dans d'autres tests, elle peut être très différente.
L'ensemble des valeurs observées vobs pour lesquelles l'hypothèse nulle H0 est admissible (non-rejetée) forme la région d'acceptation ou de non-rejet et les autres valeurs constituent la région de rejet ou domaine de rejet ou région critique.
Comme expliqué ci-dessus, cette région critique est constituée par le sous-ensemble des valeurs de la distribution d'échantillonnage qui sont si extrêmes que lorsque H0 est vrai, la probabilité que l'échantillon observé ait une valeur parmi celles-ci est très faible (la probabilité est α).
Grâce à cette modélisation mathématique, nous pouvons dès lors quantifier l'erreur commise en affirmant que la différence observée n'est pas dûe au hasard : l'erreur α est la probabilité que ce soit en réalité dû au hasard.
Cette erreur est choisie arbitrairement (en général α = 0,05) et c'est tout l'intérêt de procéder de cette manière (chercher à rejeter H0) : sous réserve que le test soit validé, nous avons le contrôle de l'erreur (puisqu'on la choisit arbitrairement).
Remarquons que dans un test unilatéral, la région de rejet est entièrement située à une des extrémités de la distribution d'échantillonnage, alors que dans un test bilatéral, cette région est située aux deux extrémités de la distribution.
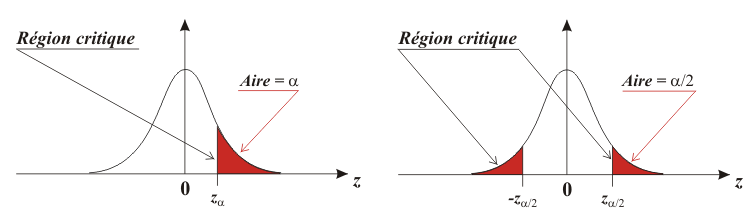
La taille de cette région de rejet est définie par α. Si α = 0,05, la taille de la région de rejet correspond à 5% de l'espace inclus dans la courbe de la distribution d'échantillonnage.
On rejette donc l'hypothèse initiale (H0) si vobs ∈ RH0(α) ou, de façon équivalente, si p-valeur(vobs) < α (voir plus p-valeur).
Le calcul de vobs et la détermination des bornes (zα, zα/2 et -zα/2 sur la figure) est dépendante du test considéré.
Les bornes sont appelées « valeurs critiques » (respectivement vcrit, vcrit,sup et vcrit,inf).