On cherche à comparer une proportion π dans une population à une certaine valeur π0 fixée à priori. On veut savoir si le fait que π soit différent de π0 est dû au hasard ou à, par exemple, la technique employée.
Ce test peut être bilatéral ou unilatéral.
La variable dépendante doit être nominale binaire (oui/non) et les valeurs regroupées pour former une variable quantitative.
L'échantillon doit être unique car il s'agit d'un test de conformité.
La taille de l'échantillon doit être ≥ 30.
Exemple :
Sur 95 naissances, on relève 53 garçons.

Cette observation est-elle conforme à l'hypothèse selon laquelle la probabilité d'avoir un garçon à la naissance est de 0,5 au seuil 95% ?
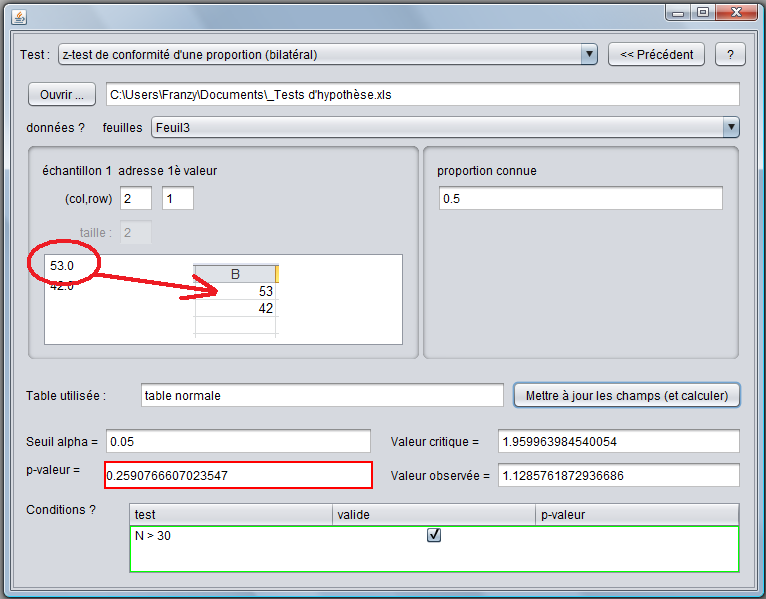
Le programme nous fournit les données suivantes :
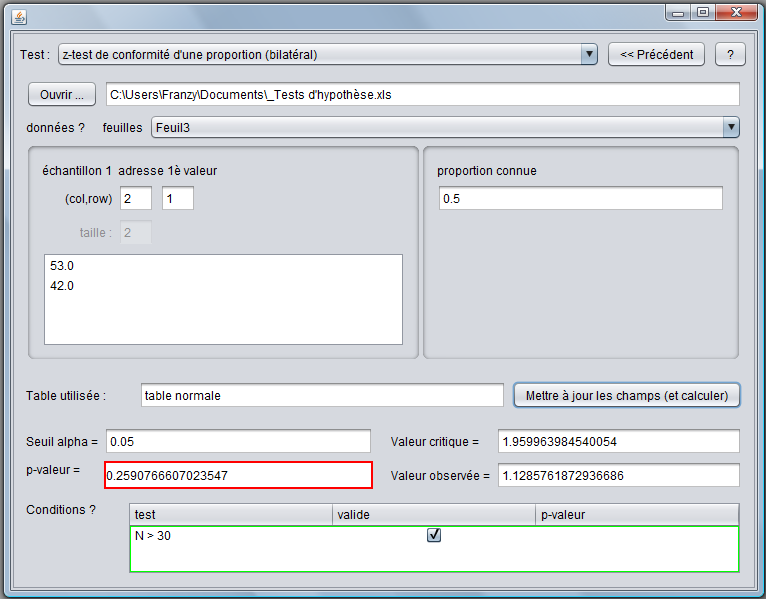
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des proportions ne peut être rejetée. L'observation ne permet donc pas de rejeter l'hypothèse selon laquelle la probabilité d'avoir un garçon à la naissance est de 0,5.
Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.
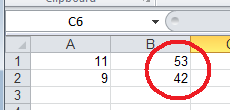
Veillez à ordonner correctement les valeurs comme indiqué sur le feuillet Excel :