On cherche à comparer les distributions de 2 échantillons indépendants. Ce test compare les fréquences cumulées F(x) des valeurs x des échantillons. Autrement dit, ce qui revient à comparer plus spécifiquement la position médianes ainsi que la dispersion des résultats.
Ce test est bilatéral.
La variable dépendante doit être qualitative ordinale.
Les effectifs des deux échantillons ne sont pas forcément identiques.
Exemple :
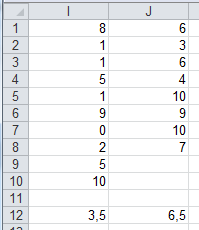
Pour étudier l'influence d'un traitement, on prélève au hasard 18 personnes désireuses de participer à cette étude et on les répartit aléatoirement dans 2 groupes distincts. On applique le traitement A au groupe 1 et le traitement B au groupe 2. A l'issue des traitements, on demande à chaque participant d'estimer son bien-être sur une échelle de 1 à 10 :

Nous voyons que les médianes n'ont pas la même valeur. La différence observée entre les 2 traitements est-elle donc significative au seuil 95% ?
Le programme nous fournit les données suivantes :
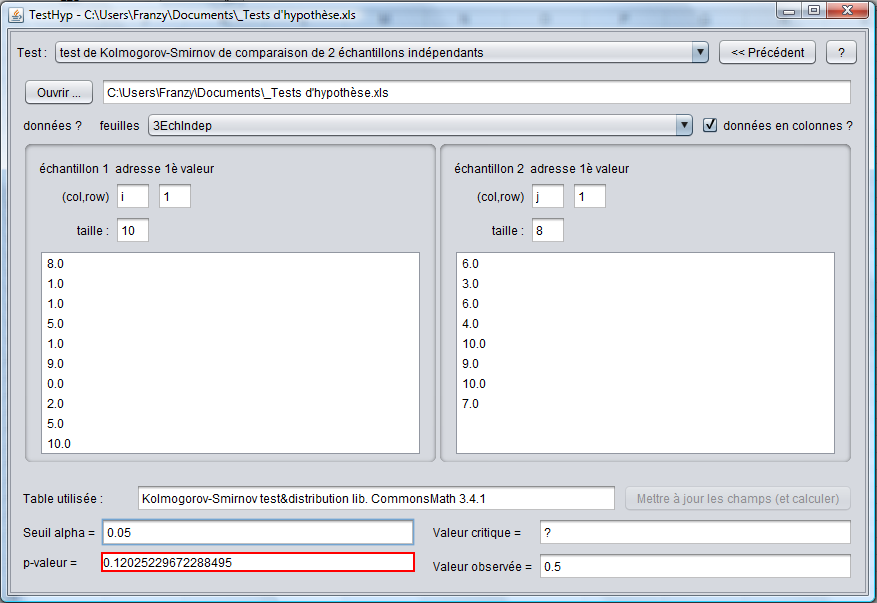
Nous pouvons voir que la pval est > au seuil α donc l'hypothèse de l'égalité des distributions (et donc des médianes) ne peut être rejetée.
Ce faisant, nous introduisons une erreur de seconde espèce β qu'il convient de ne pas oublier.